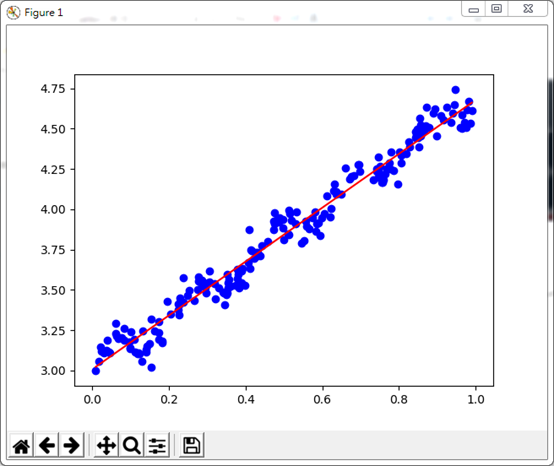
該範例摘自<<機器學習-算法原理與編程實踐>>,主要是告訴我們對於資料集的分佈趨勢,我們可以用"最小二乘法"求得回歸線(資料分佈趨勢線),然該法僅適用於線性回歸函數Y = aX + b . 但藉由這個實例亦可以看出我們可以用最小二乘法做為線性回歸資料集的預測算法,從中找出線性資料分佈的合理函數,進而預測資料分佈趨勢。
[資料集] Input File = regdataset.txt
0.635975 4.093119
0.552438 3.804358
0.855922 4.456531
0.083386 3.187049
0.975802 4.506176
0.181269 3.171914
0.129156 3.053996
0.605648 3.974659
0.301625 3.542525
0.698805 4.234199
0.226419 3.405937
0.519290 3.932469
0.354424 3.514051
0.118380 3.105317
0.512811 3.843351
0.236795 3.576074
0.353509 3.544471
0.481447 3.934625
0.060509 3.228226
0.174090 3.300232
0.806818 4.331785
0.531462 3.908166
0.853167 4.386918
0.304804 3.617260
0.612021 4.082411
0.620880 3.949470
0.580245 3.984041
0.742443 4.251907
0.110770 3.115214
0.742687 4.234319
0.574390 3.947544
0.986378 4.532519
0.294867 3.510392
0.472125 3.927832
0.872321 4.631825
0.843537 4.482263
0.864577 4.487656
0.341874 3.486371
0.097980 3.137514
0.757874 4.212660
0.877656 4.506268
0.457993 3.800973
0.475341 3.975979
0.848391 4.494447
0.746059 4.244715
0.153462 3.019251
0.694256 4.277945
0.498712 3.812414
0.023580 3.116973
0.976826 4.617363
0.624004 4.005158
0.472220 3.874188
0.390551 3.630228
0.021349 3.145849
0.173488 3.192618
0.971028 4.540226
0.595302 3.835879
0.097638 3.141948
0.745972 4.323316
0.676390 4.204829
0.488949 3.946710
0.982873 4.666332
0.296060 3.482348
0.228008 3.451286
0.671059 4.186388
0.379419 3.595223
0.285170 3.534446
0.236314 3.420891
0.629803 4.115553
0.770272 4.257463
0.493052 3.934798
0.631592 4.154963
0.965676 4.587470
0.598675 3.944766
0.351997 3.480517
0.342001 3.481382
0.661424 4.253286
0.140912 3.131670
0.373574 3.527099
0.223166 3.378051
0.908785 4.578960
0.915102 4.551773
0.410940 3.634259
0.754921 4.167016
0.764453 4.217570
0.101534 3.237201
0.780368 4.353163
0.819868 4.342184
0.173990 3.236950
0.330472 3.509404
0.162656 3.242535
0.476283 3.907937
0.636391 4.108455
0.758737 4.181959
0.778372 4.251103
0.936287 4.538462
0.510904 3.848193
0.515737 3.974757
0.437823 3.708323
0.828607 4.385210
0.556100 3.927788
0.038209 3.187881
0.321993 3.444542
0.067288 3.199263
0.774989 4.285745
0.566077 3.878557
0.796314 4.155745
0.746600 4.197772
0.360778 3.524928
0.397321 3.525692
0.062142 3.211318
0.379250 3.570495
0.248238 3.462431
0.682561 4.206177
0.355393 3.562322
0.889051 4.595215
0.733806 4.182694
0.153949 3.320695
0.036104 3.122670
0.388577 3.541312
0.274481 3.502135
0.319401 3.537559
0.431653 3.712609
0.960398 4.504875
0.083660 3.262164
0.122098 3.105583
0.415299 3.742634
0.854192 4.566589
0.925574 4.630884
0.109306 3.190539
0.805161 4.289105
0.344474 3.406602
0.769116 4.251899
0.182003 3.183214
0.225972 3.342508
0.413088 3.747926
0.964444 4.499998
0.203334 3.350089
0.285574 3.539554
0.850209 4.443465
0.061561 3.290370
0.426935 3.733302
0.389376 3.614803
0.096918 3.175132
0.148938 3.164284
0.893738 4.619629
0.195527 3.426648
0.407248 3.670722
0.224357 3.412571
0.045963 3.110330
0.944647 4.647928
0.756552 4.164515
0.432098 3.730603
0.990511 4.609868
0.649699 4.094111
0.584879 3.907636
0.785934 4.240814
0.029945 3.106915
0.075747 3.201181
0.408408 3.872302
0.583851 3.860890
0.497759 3.884108
0.421301 3.696816
0.140320 3.114540
0.546465 3.791233
0.843181 4.443487
0.295390 3.535337
0.825059 4.417975
0.946343 4.742471
0.350404 3.470964
0.042787 3.113381
0.352487 3.594600
0.590736 3.914875
0.120748 3.108492
0.143140 3.152725
0.511926 3.994118
0.496358 3.933417
0.382802 3.510829
0.252464 3.498402
0.845894 4.460441
0.132023 3.245277
0.442301 3.771067
0.266889 3.434771
0.008575 2.999612
0.897632 4.454221
0.533171 3.985348
0.285243 3.557982
0.377258 3.625972
0.486995 3.922226
0.305993 3.547421
0.277528 3.580944
0.750899 4.268081
0.694756 4.278096
0.870158 4.517640
0.276457 3.555461
0.017761 3.055026
0.802046 4.354819
0.559275 3.894387
0.941305 4.597773
0.856877 4.523616
[python] minsqrt.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
from numpy import * import matplotlib.pyplot as plt def loadDataSet(filename): X = [] Y = [] fr = open(filename) """ File data sample: 0.635975 4.093119 0.552438 3.804358 0.855922 4.456531 0.083386 3.187049 0.975802 4.506176 """ for line in fr.readlines(): curLine = line.strip().split('\t') #0.635975 4.093119 X.append(float(curLine[0])) #0.635975 Y.append(float(curLine[1])) #4.093119 return X,Y def plotscatter(Xmat,Ymat,a,b,plt): fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(Xmat,Ymat,c='blue',marker='o') Xmat.sort() Yhat = [a*float(xi)+b for xi in Xmat] #calculate predict value plt.plot(Xmat,Yhat,'r') plt.show() return yhat if __name__ == "__main__": Xmat, Ymat = loadDataSet('regdataset.txt') meanX = mean(Xmat) meanY = mean(Ymat) dx = Xmat - meanX dy = Ymat - meanY sumXY = vdot(dx,dy) sqX = sum(power(dx,2)) a = sumXY/sqX b = meanY - a*meanX print("%f,%f"%(a,b)) plotscatter(Xmat,Ymat,a,b,plt) |
[結果]
PS D:\Lab\ScriptLab\ML> python minsqrt.py
1.668743, 3.007722
2018年9月17日星期一



 留言列表
留言列表

